In the morning, we began by looking over the review questions that were on yesterday's slides. Mr. K told us not to worry about the second part of those review questions as much since we didn't really go over how to do them, but we did in the afternoon to some extent.
After we had finished briefly looking over those questions, we were given the first part of our Circular Functions test. Notice how I say "first part". The reason why I say this is because tomorrow morning, we will be getting a second part to the test, which should only take us about 5 minutes to do, according to Mr. K. The second part will consist of graphing work. That was all that happened in the morning class.
Onto the afternoon class, which we had a late start on because of Mr. K talking to the principal or something. Anyways, Mr. K first started off by showing off some trippy spiral themed pictures from www.flickr.com. Then he took it one step further by showing us his newly downloaded firefox add on, PicLens, which gave him the ability to look through all the pictures in a cool way. Its hard to explain for me so if you're interested in this, go to www.piclens.com!
Okay back to math! So, we started on a new unit called Transformations. The first thing we did was look at the graph for f(x) = x^2, which looks like this:
We then looked at what would happen when 2 was added to the function to make f(x) = x^2 + 2. The graph ended up looking like this:
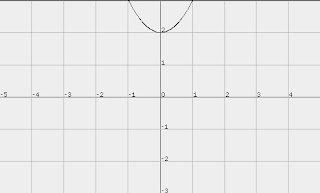
As you can see, by adding 2, the parabola was shifted upwards by two units. We then looked back at the sine graph and did the same thing to it, except we subtracted 1, therefore causing the graph to shift downwards by one unit.
Now, if you're looking at slide 3 of today's class, you'll notice that we tried graphing y(x) = 2^x. Don't fret if you don't understand what this is. The reason why the graph looks like that is because since x is equal to a number, when 2 is to the exponent of that number, it will increase as so, making the graph look like that. To help you understand it better, here is a table that shows you a simple pattern of the relationship between exponents and a number, which in this case is 2:
See the pattern? Starting from exponent 4 all the way down to negative exponent 4, the values keep halving themselves. So if x is equal to 4, that would mean the y coordinate would be 16. If x was equal to -4, that would mean the y coordinate would be at 1/16.Okay, so now that you know why it looks like that, what would the graph look like if I were to do make it f(x) = 2^(x+3)? Well, if you're still looking on that slide, then you'd see that the graph moved 3 units to the left. This is pretty much like the phase shift in those trig function graphs we did for the past few units. The only difference is that it isn't called the phase shift, since phase shift is only used when dealing with trig functions, instead, we call it the horizontal shift.
So in conclusion to this part of the afternoon class, we can say that we write these functions in the form of y = f(x-b) + a, where "b" is the horizontal shift and "a" is the vertical shift.
By the way, the weird shaped thing below the f(x) = 2^x graphs are called "piece wise functions". They are called this because of they are split into pieces. As you can see in that specific piece wise function, there are three parts to it, thus why its a piece wise function.
For the rest of the class, we were given questions to work on based on the things I just talked about. The first question, as shown in slide 6, asked us to to write f(x) = sin(x-2) + 5 in terms of g(x). Since f(x) is basically g(x) shifted 4 units to the left, the only possible answer was g(x) = sin(x+2) + 5. As you can see, the only thing that was changed was "b". To get +2, we basically just added 4 since f(x) is units to the left of g(x), meaning that we'd have to move right 4 units from f(x) to get to g(x). Simple, right?
Okay, so onto slide 9. Remember those review questions from yesterday's slide? Well, we learned how to solve those now. I'll use the same example as shown in slide 9, which was sin(2x) = 1/2. To make this easier to work with, you can Let θ = 2x and then work from there for now so that you've got sin θ = 1/2. Now, you should already know how to solve for this by now, and if you don't, look over the circular function notes again, mkay?
Yeah, so if you did it right, you should have gotten the answers in the black. If you're confused with the 13π/6 and the 7π/6, we just got those by adding 12π/6 which is equal to 2π to π/6 and the reason why we did this is because of the original 2x. Since its 2x, when you look at it on the graph, you'll see that there are two complete waves, meaning that there's going to be double the solutions. The same can be said if it was 4x instead of 2x. In the case of 4x, there'd be 8 solutions, and if it was 6x instead of 2x, there'd be 12 solutions. You see?
You think you're done with the question now eh? Well, you're not. Since you'd switched out 2x for θ, that means that you're going to have to put back the 2x. Then from there, you should be able to work with it, so if you did everything correct, you should get the answers in red. Voila, wasn't that oh so simple? :)
Um, so, I think I'm done now! Yay! Oh wait, just forgot to mention that tonight's homework is Exercise 7, questions 1-10, since you should have already finished 11-20 and if you haven't, you are a naughty child.
Now for the moment of truth, since I'm the last scribe in this cycle, that means I have a whole list to choose from now, ehehe. Therefore, I choose .....LAWRENCE.
Yeah, back to the beginning we go! Anyways, remember that there is part 2 of the Circular Functions test tomorrow, so good luck everyone!
~kristina
No comments:
Post a Comment