The Whisper Room

• The Whisper Room and What Does it Have to do with Ellipses?
• The Anatomy of the ellipse.
• The Vertical Ellipse
  
• Horizontal and Vertical Ellipse Equations
• The Pythagorean Property
• Focal Radii Property
• Sketching an Ellipse when given the equation of an ellipse and finding the length of the Major and Minor axes, The coordinates of the center, Foci's and vertices's.
• From Standard to General Form and Back Again ...

The Whisper Room and What Does it Have to do with Ellipses?

Now to start of with the question What Does The Whisper Room Have to do with Ellipses? Well the whisper room is a room found in the white house where the president of the united states lives. This room also has two marked point on the floor of the room. If you were to stand on one of those points and a friend, aunt or uncle, or anyone were to stand on the other point and if you were to say something, the other person on the other point would hear it too. Even if you whispered and talked towards any where (ex the wall) he would still here it and anyone else in between wouldn't hear it.



On the picture above or found on slide 2 of today's slides is a picture of how the whisper room in the white house works. And if you are wondering these points are called Foci points.

The Anatomy of the ellipse.





On The picture above you are probably wondering what are those numbers for. Well the numbers are our classmates measurements of a point that we picked on the edge of the ellipse, to each of the foci's, and then we added them together. We then came to a conclusion no matter where the point is the measurement of the point to each Foci and added them together the sum would be the same.


On slide four is just the The Pythagorean Property. But I will discuss that later in my blog.


On slide Five on just below the writing there is a beautiful diagram of the Anatomy of The Ellipse.





The Vertical Ellipse

Which is pretty self explanatory. If you need a visual just talk a circular device and put it in between your hands with your fingers pointing up and try squishing it together. And that is how you get an ellipse. If you need it more descriptive its where the minor axis is horizontal to the floor and where the major axis is vertical to the floor. If you do not understand me there is a vertical ellipse found on slide 6 of today's slides or you can just look at the picture below.



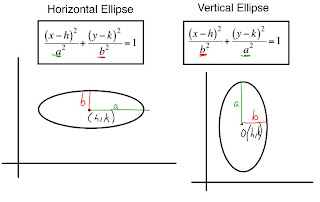
Horizontal and Vertical Ellipse Equations


The Horizontal and Vertical Ellipse Equations are almost identical but there is one thing different. On the horizontal ellipse equation it is read as: open bracket x - h closed bracket squared all over a(ey) squared plus open bracket y - k closed bracket squared all over b(bee) squared equals one . And on the vertical ellipse the a(ey) squared and b(bee) squared are switched. So it is read as: open bracket x - h closed bracket squared all over b(bee) squared plus open bracket y - k closed bracket squared all over a(ey) squared equals one.

If you need too see it written in numbers it is found on slide number seven of today's blog or just below.




The Pythagorean Property


On Slides 4 and 8 we talked a little about the Pythagorean property Regularly the Pythagorean Theory is a^ 2 + b^ 2 = c^2 but in this case of an ellipse it is c^2 + b^ 2 = a^ 2. If you don't believe me you can look below or check on slides 4 or 8 of today's slides. You need to use this property so that you can solve for the Foci because the foci is equal to c units from the center of the ellipse. Well to solve for c you will of course need to rearrange the equation which is c^2 = a^2 - b^2.




Focal Radii Property





On slide nine of today's slides and just above us there is the Focal Radii Property in action. On the first line it says the distance from any point of the circumference of the ellipse to the first foci plus the distance from the same point to the second foci is to be constantly the same. Now on the second line it says that the distance from P(pee) to foci1 plus the distance from P(pee) to foci2 is equal to the distance of A(ey)1 to foci1 plus A(ey)1 to foci2. So if that is true then the distance from A(ey)1 toFoci1 is equal to the distance of A(ey)2 to Foci2 by symmetry of course. So if that is true then the distance from P(pee) to foci1 plus the distance from P(pee) to foci2 is equal to the distance of A(ey)2 to foci2 plus A(ey)1 to foci2. And now if that is true the distance from P(pee) to foci1 plus the distance from P(pee) to foci2 is equal to 2a.


Sketching an Ellipse when given the equation of an ellipse and finding the length of the Major and Minor axes, The coordinates of the center, Foci's and vertices's.

There were some examples of these type's of questions found on slides 10 and 11 I am only going to go over one because they are practically identical on how to solve it.



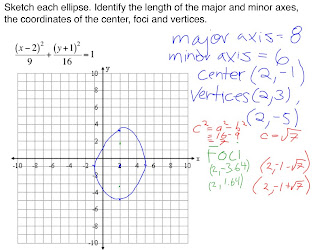
If you are given an equation the first thing that i do jot down the center on the graph and on the side of the graph , Where on an ellipse the center is (h, k) in this case the center is (2, -1). The second thing i would do is check which denominator is bigger so you know which one is a(ey) and which one is b(bee) you do this to solve for the major and minor axis. The major axis is 2a (two of ey) The bigger one in this case is 16 SO you square root it and then double it which you will get 8. For the minor axis you use the smaller number b(bee) but this time it is 2b (two of bee) so you do the same process and this time the number is 9 which become 6. To solve for the Vertices you find the end points of the major axis. in this case the Vertices are (2, 3) and (2, -5). Now the hard part The foci is tuff because you need to a little more work. This is also one of the various reasons for the Pythagorean Property. To solve for the foci point you will need to know c because the two foci points are c units away from the center. first you write down the Pythagorean Property which is c^2 = a^2 - b^2. You then plug in your given values and solve for c. In this special case the value for c is The square root of 7. The answer is found in green and red they are both correct but we would perfer to use exact values. so the one in red is the best fit answer.

Oh i almost forgot sketching the graph first you jot down the center. After you have done that you then find out if it is a vertical ellipse or a horizontal ellipse. now that you know that you can then jot down four important points. You jot down the two vertices and The two endpoints of the minor axis. For the two vertices you take half of the major axis which is the semi major-axis and then you add it to the x or y coordinates of the center depending on if it is a vertical or horizontal ellipse and you then subtract it to the x or y coordinates of the center depending if it is a vertical or horizontal ellipse. Now for the two endpoints of the minor axis you take half of the minor axis which is the semi minor-axis and then you add it to the x or y coordinates of the center depending if it is a vertical or horizontal ellipse and you then subtract it to the x or y coordinates of the center depending if it is a vertical or horizontal ellipse. After you have those points you then can draw your ellipse.

From Standard to General Form and Back Again ...

on slide 12 or just below this text is a perfect example on how to go from standard to general form and back again.





If You have an equation in standard form and you want it to make it into general form. The first thing that you would do is get rid of the denominators by multiplying it by the products of the denominators. You then expand the equation. After that you then distribute the term outside of the bracket. Then after that you rearrange the equation with the Squared variables(x^2) first then the none squared variables(x) and the the number(1)s to equal 0(zero). And there you go you get General form

Now if you have an equation in general form but you want to make it into standard form you need to first collect the like terms like (x^2 and x ) you then factor out the most common factor. After you have that you then a have some missing numbers so you then have to complete the square by taking the middle term and dividing it by 2 and then squaring it. After you have done that remember to add it on to the other side. also keep in mind to distribute the numbers. Example 16(x^2 +6x + 9) = 0 You don't just add nine to the other side you add 9 times 16 which is 144 big huge difference. after you have that you then simplify your equation and then divide it by the product of two factors on the outside of the brackets. And there you go you get standard form.

The next scriber is going to be Francis.