A more detailed rubric is here.
On Monday, April 7 you will be given a paper copy of the rubric in the picture above and you will be required to hand it in and assess yourself before I do.
Don't forget to tag your picture: pc40sw08 and trigonometry.
A window through the walls of our classroom. This is an interactive learning ecology for students and parents in my Pre-Cal Math 40S class. This ongoing dialogue is as rich as YOU make it. Visit often and post your comments freely.
A more detailed rubric is here.
On Monday, April 7 you will be given a paper copy of the rubric in the picture above and you will be required to hand it in and assess yourself before I do.
Don't forget to tag your picture: pc40sw08 and trigonometry.


Continuing to our next slide, we continue with our regular scheduled programming.
In this slide we are given sinα = 4/5 and cos β = -5 / 13 where cosα <> 0. So to find those, we know that sinβ and cosα are in quadrant 2 using Pythagoras's theorem & a picture of the unit square like so.
5² - 4² = 3² (25 - 16 = 9 --> √9 = 3) and 13² - 5² = 12 ² (169 - 25 = 144 --> √144 = 12)
It then asks us to find what Tan(α - β) is so we basically combine Sin(α - β) /Cos(α - β)
GREAT! So now we have cosα = -3/5 and sinβ = 12 / 13. So Now we can get Tan(α - β) .
I know it's homework, but I'll post up my answer so that others can compare. Correct me if I'm wrong PLEASE!
Sin(α - β) = SinαCosβ - CosαSinβ. Cos(α - β) = CosαCosβ + SinαSinβ.
Then, set it up like this. SinαCosβ - CosαSinβ/CosαCosβ + SinαSinβ.
Replace them. (4/5)(-5/13) - (-3/5)(12/13) / (-3/5)(-5/13) + (4/5)(12/13) --> (-20/65) - (36/65) / (15/65) + (48/65) --> (-56/65) / (63/65)
*MULTIPLY BY THE RECIPROCAL* (-56/65) * (65/63)
* 65's REDUCE* -56 / 63. So I got an answer of Tan(α - β) = -56 / 63
That's all for today folks! Remember, we start a new unit tomorrow!!
P.S. HEY fellow JabbaMatheez! We still have our PICTURES due after the break so don't forget that while you're all having fun and having adventures on SPRING BREAK '08!
Oh wait, there's still the masking of the next Scribe!
I will pass the Jabba Scribe on to... FRANCIS!!
~Rence OUT!










 a)Here's an equation in cose. To find D we found the average of the min and max which was 5. We can now find parameter a by subtracting 5 from the max 9.6. B=2pi/period so in our equation it'll be 2pi/12. In our graph here it does not start at the max where cosine starts so it must've moved by 4.5 our parameter c.
a)Here's an equation in cose. To find D we found the average of the min and max which was 5. We can now find parameter a by subtracting 5 from the max 9.6. B=2pi/period so in our equation it'll be 2pi/12. In our graph here it does not start at the max where cosine starts so it must've moved by 4.5 our parameter c.






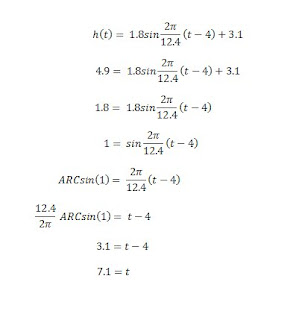 Looks difficult? Nah! Its so simple! You see, all I did was input the max value, which was 4.9 into h(t) . From there, I then solved for t. I'm sure most of you have gotten stuck after getting to the ARCsin part, well then don't fret, because I've also had troubles with that in the past. All you have to do to isolate the (t-4) is to multiply both sides by the reciprocal of 12.4/2pi. When you do this, 2pi/12.4 on the right side will get cancelled out and then you will be left with 12.4/2pi * ARCsin(1) = t - 4. From there's its baby stuff! We're all in pre cal, I don't think you need me to explain what to do from there. Anyways, I hope this solves any problems people had with slide 4. MOVING ON..
Looks difficult? Nah! Its so simple! You see, all I did was input the max value, which was 4.9 into h(t) . From there, I then solved for t. I'm sure most of you have gotten stuck after getting to the ARCsin part, well then don't fret, because I've also had troubles with that in the past. All you have to do to isolate the (t-4) is to multiply both sides by the reciprocal of 12.4/2pi. When you do this, 2pi/12.4 on the right side will get cancelled out and then you will be left with 12.4/2pi * ARCsin(1) = t - 4. From there's its baby stuff! We're all in pre cal, I don't think you need me to explain what to do from there. Anyways, I hope this solves any problems people had with slide 4. MOVING ON..